Diastereoizomeria, struktury mezo i konfiguracja względna
cykl: izomeria optyczna dla szkoły średniej
część 2 z 4

Zapraszamy na drugą część naszego cyklu o izomerii optycznej. Dzisiaj opowiemy o konfiguracji względnej, która sprawia uczniom mnóstwo problemów. Dlatego wykroczymy nieco poza zakres typowej wiedzy podręcznikowej aby poprawić zrozumienie tego tematu.

W czasie czytania artykułu należy samemu układać z „Atomków” i porównywać omawiane struktury i ich symetrię. „Atomki” są wręcz idealną pomocą do rozważań o wszelkich rodzajach izomerii – w tym optycznej.

Diastereoizomery

Stereoizomery – enancjomery i diastereoizomery

Zanim przejdziemy do głównej części dzisiejszego wpisu musimy poznać związki, które mają większą niż jeden liczbę centrów chiralności. Dzisiaj porozmawiamy o związkach mających tylko dwa centra chiralności, jednak już w kolejnej części będziemy omawiać cząsteczki mające cztery lub pięć centrów chiralności.

Rozważmy cząsteczkę 1‑bromo‑1,2‑dichloro‑2‑jodoetanu.

Zbudujmy jej model jak na zdjęciu (struktura A), a następnie jego odbicie lustrzane (struktura B). Próbując przyłożyć do siebie obydwa modele natychmiast zauważymy, że nie nakładają się one na siebie, a zatem są enancjomerami.

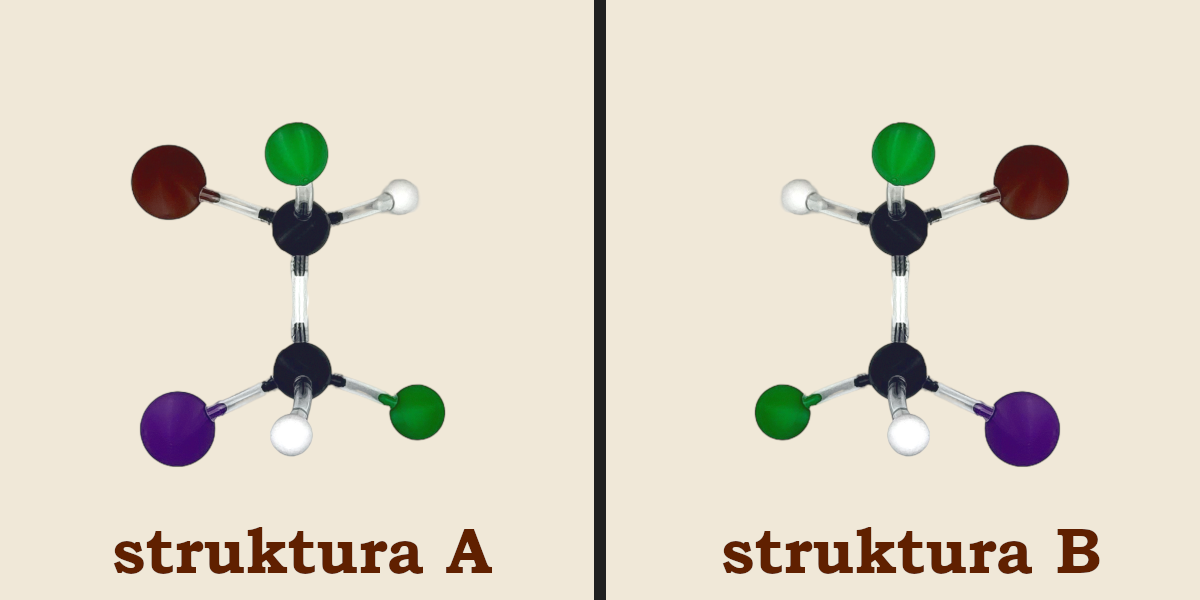
Po kilku próbach spostrzeżemy, że model tej cząsteczki możemy zbudować jeszcze inaczej (struktura C). Ten model również możemy odbić w lustrze uzyskując kolejny enancjomer (struktura D).

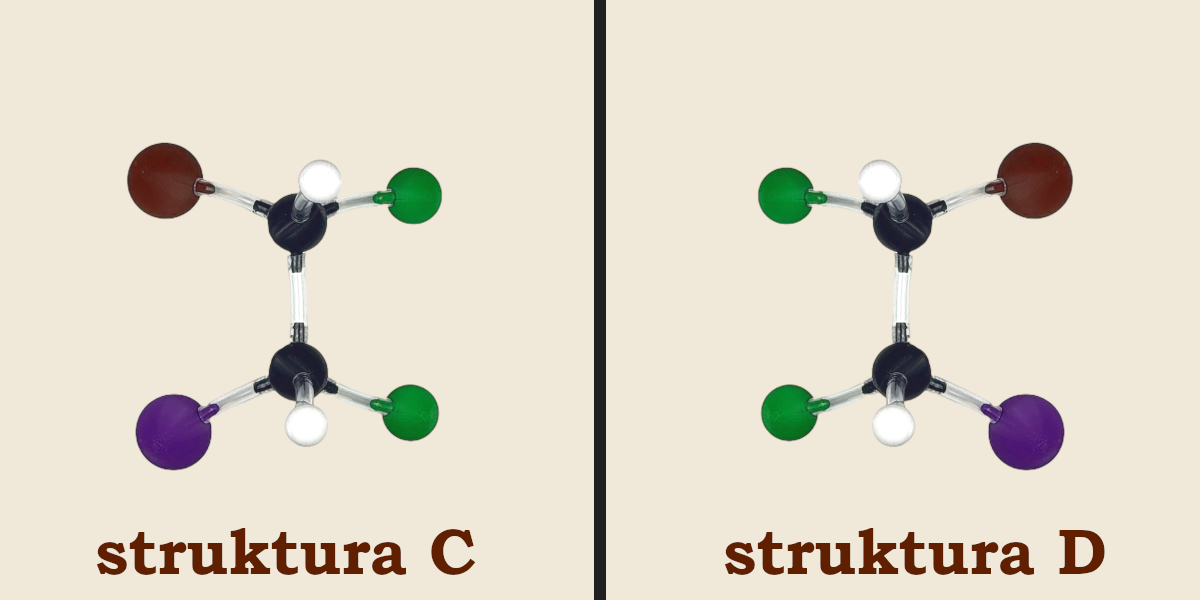
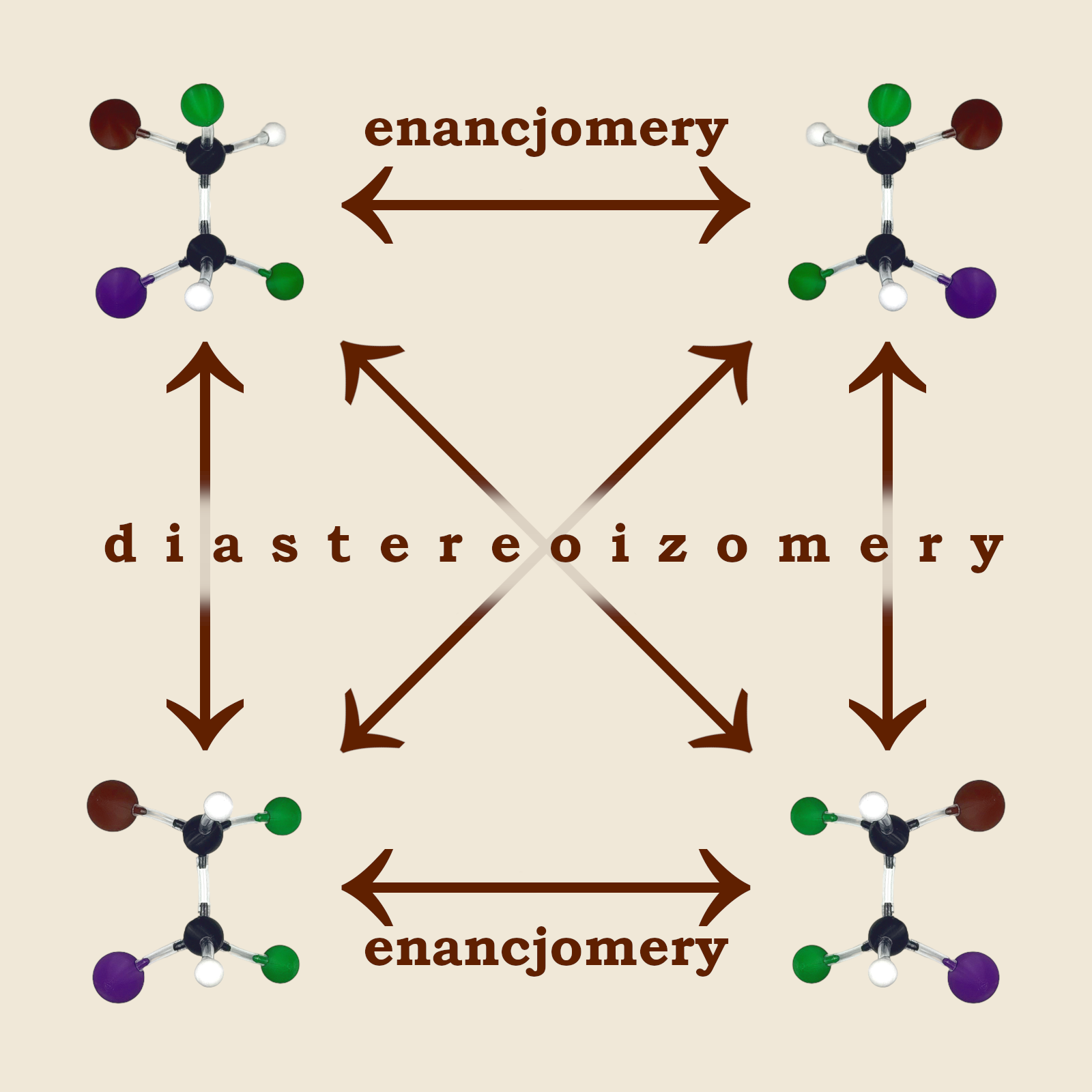
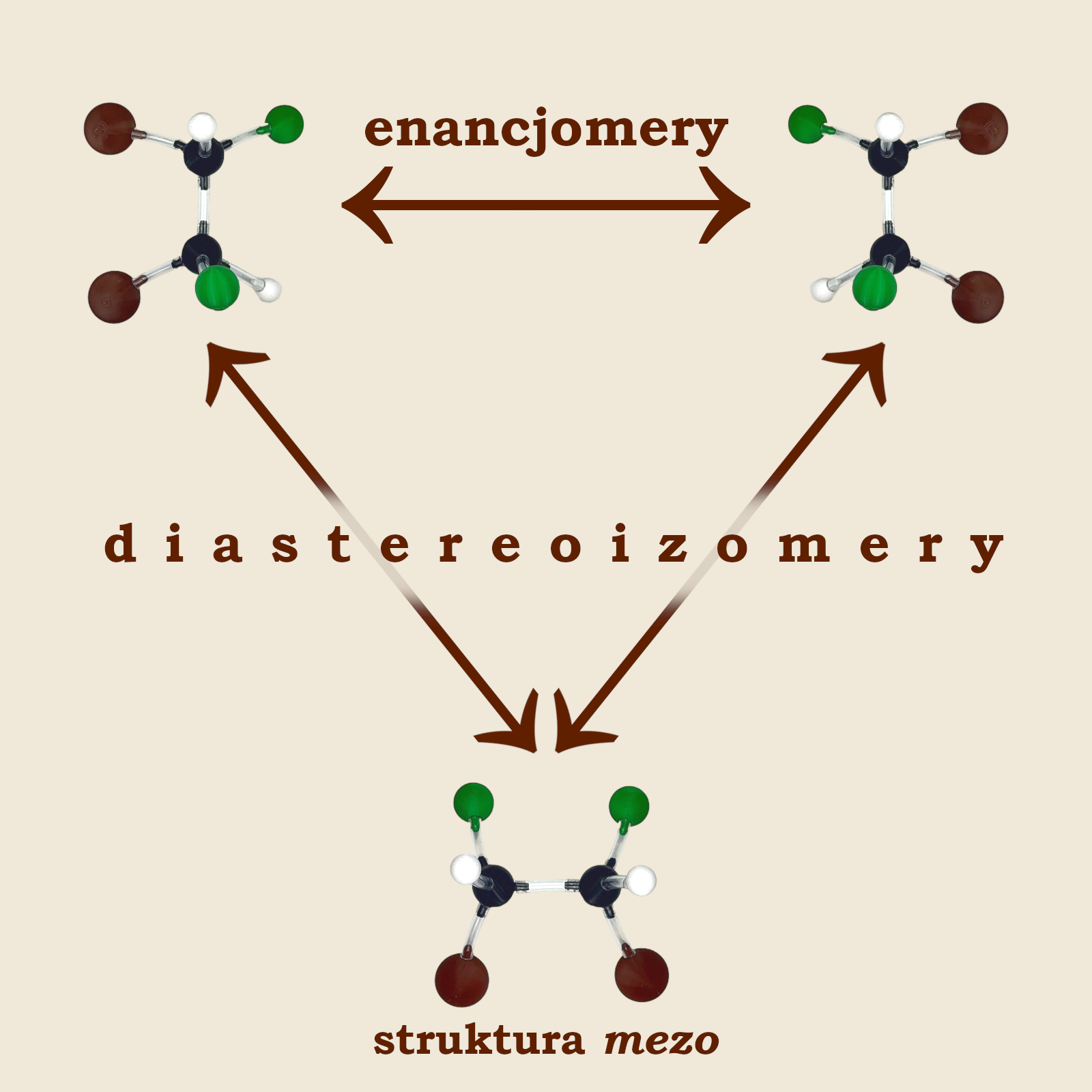
Zauważmy, że struktura C nie jest ani tożsama ze strukturami A i B, ani nie jest ich odbiciem lustrzanym. To samo można powiedzieć o strukturze D. Związki te w stosunku do siebie są stereoizomerami (czyli izomerami przestrzennymi) jednak nie są enancjomerami. Stereoizomery nie będące wzajemnymi odbiciami lustrzanymi nazywane są diastereoizomerami.

Wskazówka
W klasie można poprosić uczniów o ułożenie tego związku z „Atomków” nie dając wskazówek co do konfiguracji poszczególnych atomów węgla, a następnie wspólnie rozdzielić ułożone struktury na enancjomery i diastereoizomery.

Związek C jest diastereoizomerem związku A oraz związku B. Analogicznie – związek D jest również diastereoizomerem związku A oraz związku B. Natomiast związki A i B są w stosunku do siebie enancjomerami. Podobnie jak związki C oraz D.

Intuicja podpowiada nam, że każde kolejne centrum chiralności podwaja liczbę stereoizomerów. Tak więc związki o dwóch centrach chiralności będą miały cztery stereoizomery, o trzech centrach chiralności – osiem, o czterech centrach chiralności – szesnaście itd. Jednak nie zawsze liczba stereoizomerów związku jest łatwa do obliczenia. Stosując postęp geometryczny możemy wyznaczyć maksymalną, a nie dokładną liczbę stereoizomerów. W cząsteczce o n centrach chiralności jest ich ⩽ 2ⁿ.

Czemu tak jest? Czy jest w ogóle możliwe aby związek o dwóch centrach chiralności miał mniej niż cztery stereoizomery? Jak najbardziej tak!

Struktury mezo

Zbudujmy teraz z „Atomków” inną cząsteczkę – 1,2‑dibromo‑1,2‑dichloroetan. Jest ona podobna do poprzedniej. Ma również dwa centra chiralności. Łatwo zbudujemy pierwsze dwie struktury (struktura E i F), będące w stosunku do siebie enancjomerami.

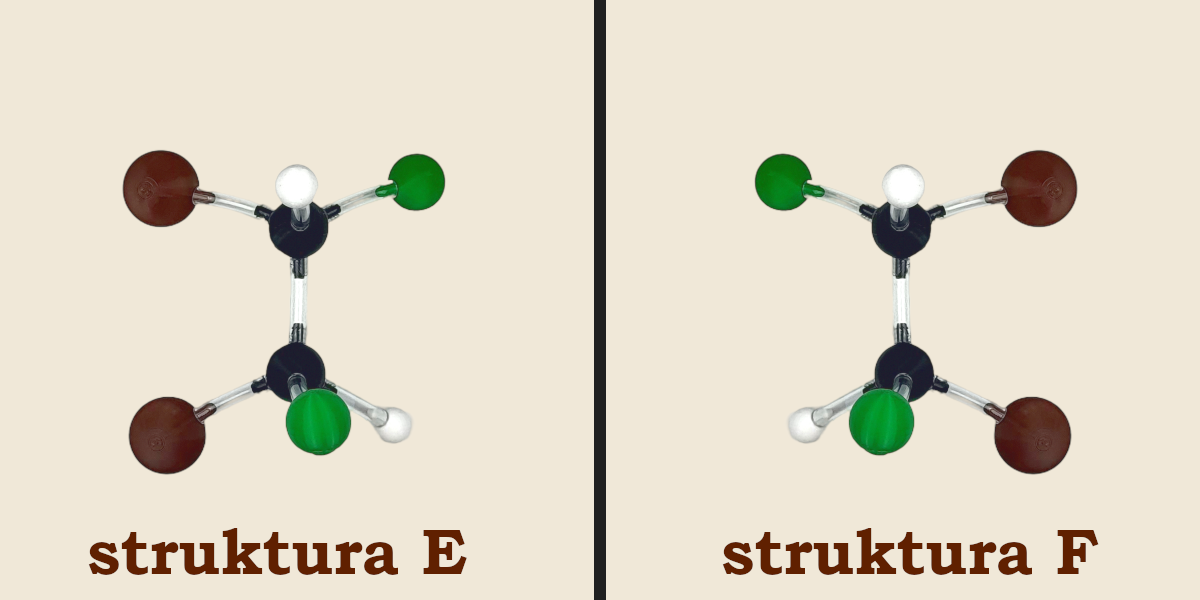
Teraz spróbujmy znaleźć diastereoizomer struktury E (struktura G), a następnie odbić go w lustrze w celu stworzenia jego enancjomeru (struktura H). Po zbudowaniu struktur G i H przyjrzyjmy się im uważnie. Okaże się, że jest to... ta sama cząsteczka, tylko obrócona o 180°.

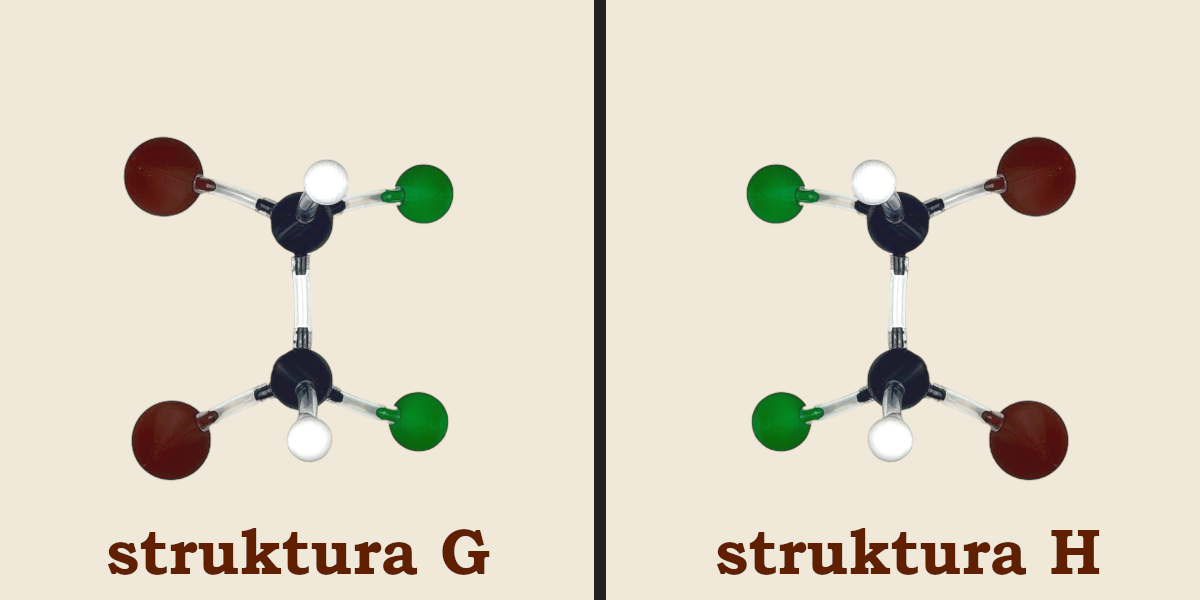
Ponieważ struktury G i H to jedna i taka sama cząsteczka, więc związek ten ma tylko trzy stereoizomery (struktury E, F i G)!

Zbudowany przez nas stereoizomer nazywamy dodając do nazwy przedrostek mezo–. Nie skręca on światła, a zatem nie jest optycznie czynny. Jest tak, gdyż cząsteczka ta ma płaszczyznę symetrii – oba jej końce stanowią swoje lustrzane odbicie. A więc konfiguracja bezwzględna obu atomów węgla w tej cząsteczce jest zawsze przeciwna. Możemy ją alternatywnie zapisać na dwa równorzędne sposoby; stosując przedrostek (S,R)— lub (R,S)—. Zatem światło przechodząc przez tę substancję napotyka na tyle samo identycznych (to ważne!) centrów chiralności skręcających płaszczyznę światła o pewien kąt w lewo, jak i w prawo. W wyniku tego efekt skręcenia się znosi. Dokładnie tak samo jak w mieszaninie racemicznej.

Podsumowanie

Związki mające n centrów chiralności najczęściej mają 2ⁿ stereoizomerów. Istnieją jednak związki, które mają ich mniej. Dzieje się tak wtedy, gdy pomiędzy tymi centrami chiralności znajduje się płaszczyzna symetrii. Wtedy jeden lub więcej stereoizomerów nie mają swoich enancjomerów. Takie struktury nazywamy strukturami mezo.

Konfiguracja względna

Powiązania związków optycznie czynnych

Wróćmy do cząsteczki, której przykład podawałem już w poprzednim wpisie – (S)‑(—)‑2‑metylo‑1‑butanolu. W wyniku działania na ten alkohol chlorowodorem otrzymamy chlorek alkilu, czyli (S)‑(+)‑1‑chloro‑2‑metylobutan.

W tej reakcji nie pęka żadne wiązanie przy chiralnym atomie węgla. Zatem z danego enancjomeru substratu powstanie konkretny i zawsze ten sam enancjomer produktu. Między tymi dwoma związkami zachodzi więc wzajemna zależność.

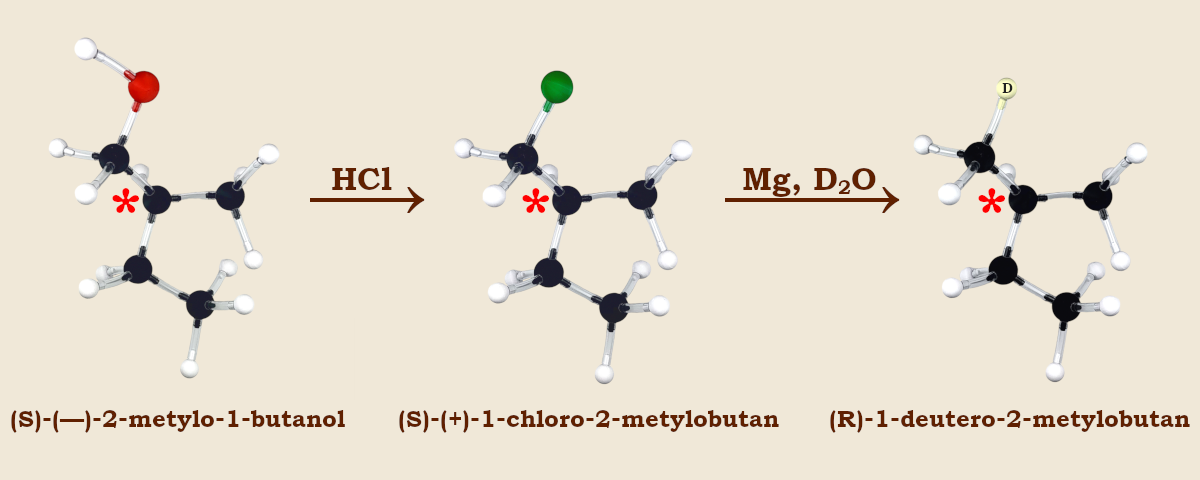
Zwróćmy uwagę, że zmieniła się skrętność z lewoskrętnej na prawoskrętną. Nie zmieniła się wprawdzie konfiguracja absolutna, ale to tylko zbieg okoliczności wynikający z faktu, że „ważność” podstawnika —CH₂OH jest identyczna jak —CH₂Cl. Jeżeli teraz poprowadzimy syntezę dalej, mieszając nasz chlorek alkilu z wiórkami magnezu, a następnie otrzymany odczynnik Grignarda hydrolizując w ciężkiej wodzie (D₂O), to w miejsce —CH₂Cl uzyskamy podstawnik —CH₂D. Będzie on już mniej „ważny” niż grupa etylowa i konfiguracja absolutna zmieni się na R. Nadal jednak wszystkie te trzy związki będą należeć do jednej rodziny enancjomerów wzajemnie od siebie zależnych.

Koniecznie ułóż te cząsteczki z „Atomków” i samodzielnie sprawdź ich konfigurację absolutną trzymając za „najmniej ważny” podstawnik (czyli atom wodoru) przy chiralnym atomie węgla. Centra chiralności zaznaczone są na zdjęciu czerwoną gwiazdką. Atom deuteru zasymuluj oznaczając jeden z atomów wodoru zmywalnym flamastrem.
Do ułożenia tych cząsteczek i „wirtualnego” przeprowadzenia opisanych reakcji wystarczy nawet podstawowy (100‑elementowy) zestaw do chemii organicznej.

Jeżeli zmienimy konfigurację substratu na przeciwną, to na przeciwne zmienią się również konfiguracje wszystkich produktów omówionych wyżej reakcji. Powstaną w ten sposób dwa równoległe łańcuchy wzajemnych zależności pomiędzy związkami o różnej skręcalności i różnej konfiguracji bezwzględnej, jednak leżących w jednym ciągu reakcji chemicznych.

Empiryczne ustalanie konfiguracji absolutnej

Poprzedni artykuł w tym cyklu zakończyliśmy konkluzją, że konfiguracja absolutna nie ma bezpośredniego związku z rzeczywistą skręcalnością optyczną enancjomeru. Skąd więc wiemy, jaką konfigurację absolutną ma dana cząsteczka chiralna? Umiemy łatwo zmierzyć jej skręcalność, jednak ustalenie rzeczywistej struktury cząsteczki nie wydaje się już takie proste.

I rzeczywiście – jest to zagadnienie mocno skomplikowane. Chemik nie może przez lupę czy mikroskop podejrzeć jak zbudowana jest dana cząsteczka. Określenie jej dokładnej struktury wymaga żmudnych badań spektroskopowych i jest trudne oraz pracochłonne.

Dlatego aż do roku 1949 nie udało się ustalić konfiguracji absolutnej żadnego optycznie czynnego związku. Dopiero wtedy Johannes Martin Bijvoet – dyrektor Laboratorium van’t Hoffa Uniwersytetu w Utrechcie – prowadząc badania rentgenograficzne po raz pierwszy ustalił konfigurację absolutną soli kwasu (+)‑winowego.

To był długo oczekiwany przełom!

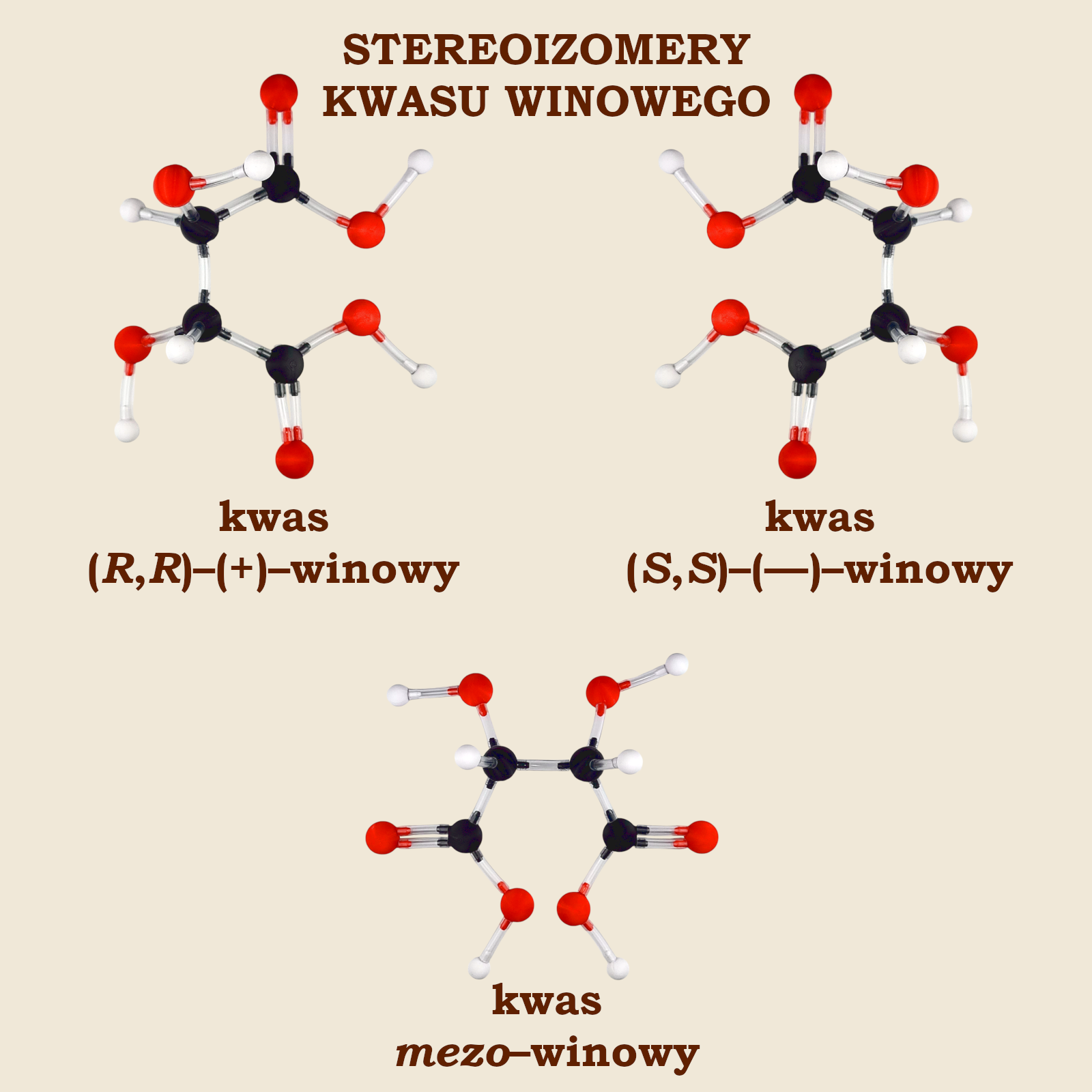
Kwas winowy to kwas dwukarboksyowy z dwoma dodatkowymi grupami –OH (tzw. hydroksykwas). Ma on trzy stereoizomery, których konfiguracje prezentujemy na ilustracji powyżej.

Łańcuchy związków wzajemnie zależnych – konfiguracja względna

Choć – jak wspomniałem – określanie dokładnej struktury związków jest bardzo trudne, to od razu po ustaleniu konfiguracji absolutnej kwasu (+)‑winowego ustalono również konfigurację setek innych związków. W jaki sposób? Właśnie dzięki opisanym wcześniej łańcuchom wzajemnych zależności. Znano już wtedy łańcuchy zależności liczące setki, a nawet tysiące związków, więc błyskawicznie określono konfiguracje absolutne ich wszystkich.

Do tego tematu jeszcze wrócimy w następnej części cyklu.

Podsumowanie

Zależność pomiędzy konfiguracjami dwóch optycznie czynnych związków można ustalić przekształcając jeden związek w drugi za pomocą reakcji, w których nie zachodzi rozerwanie wiązania z atomem chiralnym. Powstają tak dwa równoległe łańcuchy enancjomerów. Mówimy, że w każdym z tych łańcuchów znajdują się związki o tej samej konfiguracji względnej.

Związki o tej samej konfiguracji względnej mogą mieć różną skręcalność światła, a także różną konfigurację absolutną. Jednak należą do jednego łańcucha związków wzajemnie od siebie zależnych, co z punktu widzenia chemika czasami jest dużo ważniejsze. Szczególnie zaś ważne jest to dla substancji występujących w organizmach żywych.

Wskazówki praktyczne

Do dzisiejszej lekcji i rozważań na temat konfiguracji względnej gorąco polecam zestaw rozszerzony (200‑elementowy) do chemii organicznej. Posiada on dużą liczbę heteroatomów, z których można budować różne podstawniki. Do jednoczesnej budowy struktur ze zdjęć przydadzą się dodatkowe atomy chloru, bromu i jodu wzięte np. z rozszerzonego zestawu nieorganicznego.

🧐 Zobacz też 🧐

Wszystkie artykuły cyklu o izomerii optycznej:

• Cykl o izomerii optycznej – Skręcalność optyczna i konfiguracja absolutna (część 1 z 4),
• Cykl o izomerii optycznej – Diastereoizomeria, struktury mezo i konfiguracja względna (część 2 z 4) ← tu jesteś,
• Cykl o izomerii optycznej – Projekcja Fishera, konfiguracja D i L, enancjomeria cukrów i aminokwasów (część 3 z 4) (w przygotowaniu),
• Cykl o izomerii optycznej – Cyklizacja cukrów, hemiacetale, anomery, mutarotacja (część 4 z 4) (w przygotowaniu),

Łukasz Aranowski
22 kwietnia 2024