Skręcalność optyczna i konfiguracja absolutna
cykl: izomeria optyczna dla szkoły średniej
część 1 z 3

„Atomki” to wspaniała pomoc w nauce chemii. Przydają się w najróżniejszych zastosowaniach. Trudno jednak wymarzyć sobie lepszy moment do ich użycia niż nauka zagadnień związanych z izomerią optyczną. Są wręcz wymarzonym wsparciem dla opanowania tych zagadnień.

Izomeria optyczna (enancjomeria) sprawa bardzo wiele problemów zarówno uczniom jak i nauczycielom. Uczniom – w jej przyswojeniu, a nauczycielom – w jej przystępnym wytłumaczeniu. W naszej serii artykułów przejdziemy przez te wszystkie zagadnienia krok po kroku. Zobaczycie jak łatwo je opanować dzięki „Atomkom”. Zaczniemy od najprostszych przykładów, a skończymy na skomplikowanych cząsteczkach organicznych ze szczególnym uwzględnieniem wzorów rzutowych Fischera dla cukrów.

Dzisiaj część pierwsza  – czynność optyczna i konfiguracja bezwzględna.

Czynność optyczna

Odkrycie skręcalności

W 1815 fizyk Jean‑Baptiste Biot przypadkowo odkrył, że kryształy pewnych substancji powodują skręcenie płaszczyzny polaryzacji światła. Jednak dopiero w 1848 Ludwik Pasteur rozdzielając za pomocą lupy i pęsety dwa rodzaje kryształków kwasu winowego spostrzegł, że po rozpuszczeniu ich w wodzie, otrzymane roztwory nadal powodują skręcenie płaszczyzny polaryzacji światła.

Przedstawił więc hipotezę, że ta własność wynika nie tyle ze specyfiki kryształów ile z budowy samych cząsteczek. Muszą więc istnieć cząsteczki, które różnią się od siebie tylko tym, że są swoimi odbiciami lustrzanymi. Zupełnie jak prawa i lewa rękawiczka.

Pomiary skręcalności

Skręcenie płaszczyzny polaryzacji światła przez daną substancję wykrywamy za pomocą polarymetru. W skrócie, jego działanie polega na przepuszczeniu wiązki spolaryzowanego światła monochromatycznego przez rurkę zawierającą badaną substancję. Na końcu urządzenia jest analizator, który obracany jest pod odpowiednim kątem tak aby ustalić płaszczyznę maksymalnego natężenia odbieranego światła.

Jeżeli substancja skręca płaszczyznę polaryzacji światła w prawo (zgodnie z ruchem wskazówek zegara), to nazywamy tę substancję „prawoskrętną” i przyjmujemy, że kąt skręcalności jest dodatni. Do nazwy substancji dopisujemy przedrostek (+) – np. kwas (+)‑mlekowy lub (+)‑2‑metylo‑1‑butanol. Jeżeli substancja skręca płaszczyznę polaryzacji światła w lewo (przeciwnie do ruchu wskazówek zegara), to nazywamy tę substancję „lewoskrętną” i przyjmujemy, że kąt skręcalności jest ujemny. Do nazwy substancji dopisujemy przedrostek (—) – np. kwas (—)‑mlekowy lub (—)‑2‑metylo‑1‑butanol. Izomery jednego związku skręcające światło w dwie różne strony nazywamy enancjomerami.

Skąd się bierze skręcalność?

Jaki jest mechanizm skręcania płaszczyzny polaryzacji światła przez określone substancje? Dlaczego tylko substancje mające cząsteczki nienakładalne na siebie po odbiciu w lustrze mają tę własność?

W tak postawionym pytaniu tkwi pewna nieścisłość. Jeżeli zbadamy skręcalność światła np. w kwasie mlekowym, to najczęściej jej nie wykryjemy. Jest tak, gdyż analizowany kwas mlekowy jest mieszaniną racemiczną (inaczej: racematem; czyli równomolową mieszaniną cząsteczek skręcających światło w lewą i w prawą stronę). Dopiero po rozdzieleniu enancjomerów zaobserwujemy skręcalność.

Na poziomie mikroskopowym w zasadzie każda cząsteczka zaburza płaszczyznę polaryzacji światła. Światło przechodząc przez pojedynczą cząsteczkę skręca swoją płaszczyznę polaryzacji o niewielką wartość oddziałując z jej fragmentami obdarzonymi ładunkiem. Jednak ze względu na nieuporządkowane rozmieszczenie dużej liczby cząsteczek wchodzących w skład próbki, dla każdej cząsteczki „napotkanej” przez promień światła, na drodze promieniowi stanie też cząsteczka zorientowana tak, że stanowi jej lustrzanej odbicie. W ten sposób efekt skręcenia zostaje zniesiony. Związek jest optycznie nieczynny. Wynika to nie tyle z własności pojedynczej cząsteczki, co z nieuporządkowanego ustawienia wielu cząsteczek.

Zatem substancje zawierające nieuporządkowane cząsteczki stanowiące dla siebie nawzajem odbicie lustrzane będą nieczynne optycznie bez względu na to, czy te cząsteczki po odbiciu w lustrze da się nałożyć na siebie (czyli są to takie same cząsteczki, tylko inaczej obrócone), czy nie (czyli są enancjomerami). Jednak w tym drugim przypadku da się fizycznie rozdzielić cząsteczki od ich lustrzanych odbić i uzyskać substancję czynną optycznie.

Budowa cząsteczek chiralnych

Przechodzimy do praktyki. Jeżeli nasi podopieczni jeszcze nie wiedzą jaki warunek musi spełnić cząsteczka aby jej odbicie w lustrze nie było identyczne, to rozdajemy uczniom zestawy i proponujemy aby wymyślili to sami. Uprzedzamy uczniów, że cząsteczka nie powinna być bardzo skomplikowana (np. ustalmy, że powinna liczyć mniej niż 10 atomów). Wymyślenie warunku chiralności wcale nie jest łatwym zadaniem!

Okazuje się, że jedynym sposobem na uzyskanie takiej cząsteczki jest użycie atomu węgla o hybrydyzacji sp³ posiadającego cztery różne podstawniki. Cząsteczkę taką nazywamy cząsteczką chiralną, a atom węgla z czterema różnymi podstawnikami – centrum chiralności.

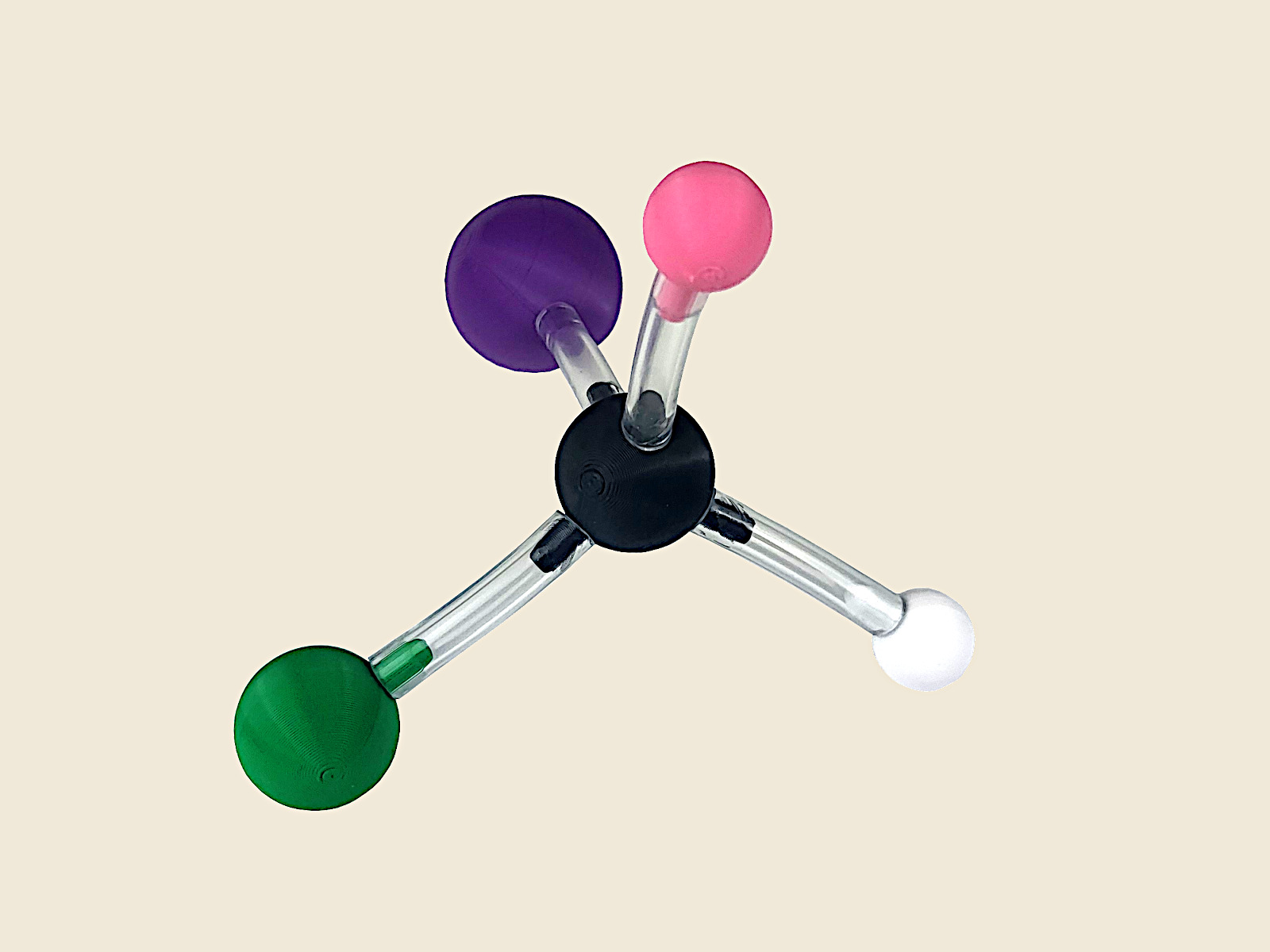
Do tego ćwiczenia nadają się dowolne zestawy do chemii organicznej. Jako podstawników uczniowie mogą używać (w zależności od zestawu) pojedynczych atomów: wodoru, fluoru, chloru, jodu oraz grup: wodorotlenowej, karboksylowej, aminowej, metylowej, nitrowej, nitrylowej itd.

Moglibyśmy wnioskować, że wszystkie cząsteczki posiadające jeden lub więcej atomów węgla o różnych podstawnikach (czyli jedno lub więcej centrów chiralności) będą miały optycznie czynne enancjomery. Niestety, to byłby wniosek pochopny. W kolejnych częściach cyklu przedstawimy wyjątek od tej reguły – achiralne cząsteczki o parzystej liczbie symetrycznie położonych centrów chiralności.

Konfiguracja absolutna (bezwzględna)

Określanie konfiguracji R i S

W jaki sposób możemy opisać konfigurację cząsteczki zawierającej centrum chiralności prościej niż poprzez jej narysowanie? W latach 50‑tych XX wieku trzech pionierów badań nad stereoizomerią – R. S. Cahn, C. Ingold i V. Prelog – umówiło się na pewną metodę, która jednoznacznie pozwala określić budowę takiej cząsteczki.

1. Grupujemy wszystkie podstawniki w kolejności ich pierwszeństwa. Reguły pierwszeństwa opiszemy dalej.
2. Spoglądamy na cząsteczkę tak, aby podstawnik o najmniejszym pierwszeństwie (najmniej ważny) był schowany za atomem węgla stanowiącym centrum chiralności (był jak najdalej od nas).
3. Sprawdzamy kolejność pozostałych widocznych podstawników zaczynając od najważniejszego. Jeżeli ich ważność maleje posuwając się zgodnie ze wskazówkami zegara, to przypisujemy cząsteczce konfigurację absolutną R (łac. rectus – prawy). Jeżeli zaś maleje w kierunku przeciwnym do ruchu wskazówek zegara, to przypisujemy cząsteczce konfigurację S (łac. sinister – lewy).

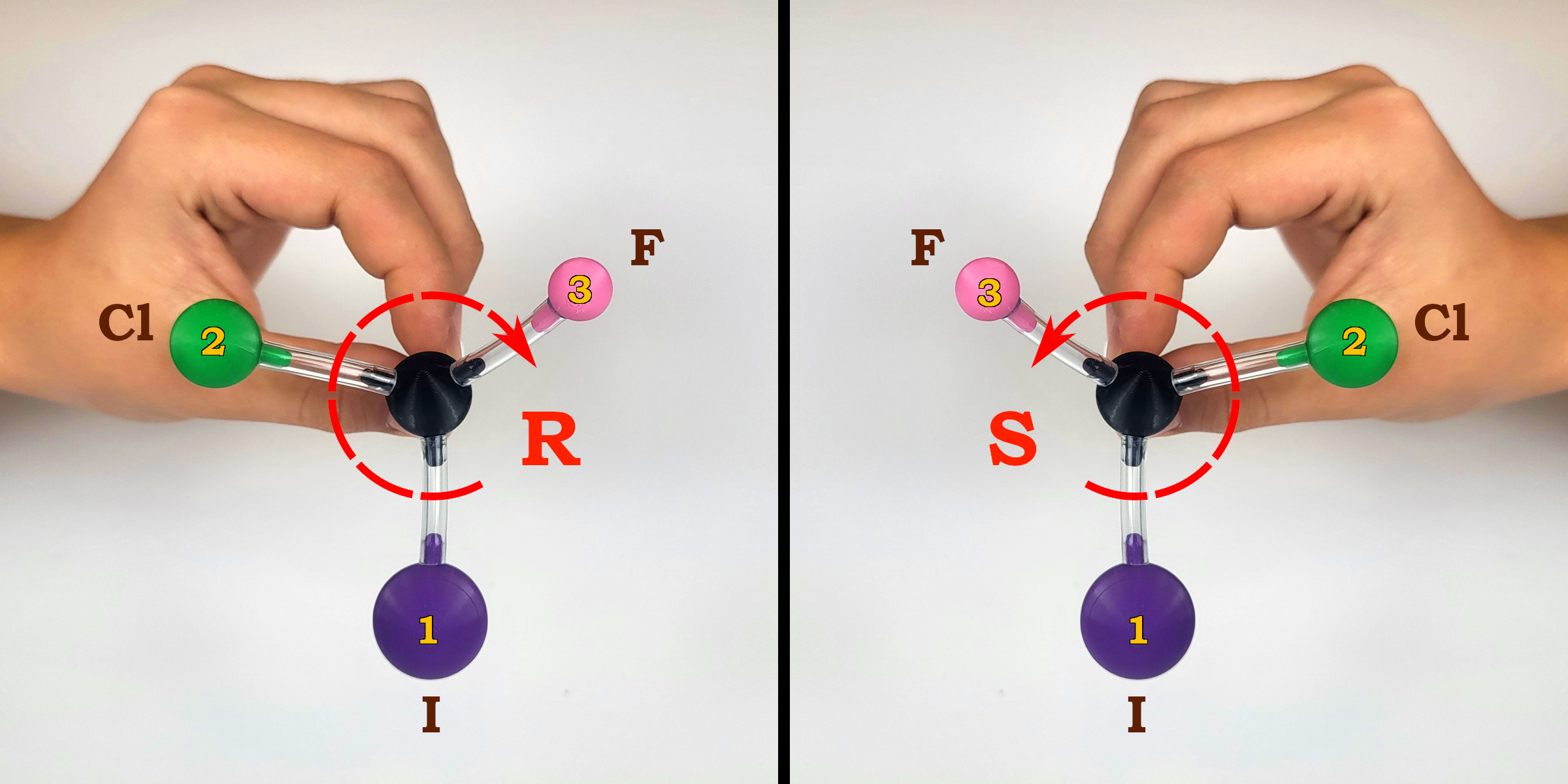
Reguły pierwszeństwa podstawników

1. Jeżeli wszystkie cztery atomy podłączone do centrum chiralności są różne, to ich pierwszeństwo zależy od liczb atomowych, a w dalszej kolejności (w przypadku różnych izotopów) od liczb masowych. Pierwszeństwo ma atom o wyższej liczbie (najpierw atomowej, później masowej). Np. —Br > —Cl > —¹³CH₃ > —¹²CH₃.
2. Jeżeli na podstawie reguły 1 nie da się ustalić pierwszeństwa to badamy atomy z kolejnej strefy koordynacyjnej (czyli te połączone bezpośrednio z atomem łączącym się z centrum chiralności). Układamy je w kolejności malejącej liczby atomowej i masowej, a następnie sprawdzając kolejne miejsca na otrzymanych listach szukamy pierwszej różnicy.
   Pokażmy to na przykładach:
   1. Grupa —C₂H₅ jest ważniejsza niż —CH₃, bo już na pierwszym miejscu listy atomów drugiej strefy koordynacyjnej ułożonych w kolejności ważności znajdują się dwa różne atomy; (C, H, H) w grupie etylowej i (H, H, H) w grupie metylowej.
   2. Grupa —CClH₂ jest ważniejsza niż —C(CH₃)₂H, bo stojący na pierwszym miejscu atom chloru (Cl, H, H) ma większą liczbę atomową od znajdującego się na pierwszym miejscu atomu węgla (C, C, H).
   3. Grupa —CCl₂H jest ważniejsza niż —CClFH, bo stojący na drugim miejscu atom chloru (Cl, Cl, H) ma większą liczbę atomową od znajdującego się na drugim miejscu atomu fluoru (Cl, F, H).
   Warto zaproponować uczniom samodzielne ułożenie z „Atomków” i zbadanie powyższych przykładów.
   Jeżeli badanie tej strefy koordynacyjnej nie przyniesie rezultatu przesuwamy się do następnej (czyli teraz badamy atomy oddalone od centrum chiralności o trzy wiązania), gdzie obowiązują te same reguły. I tak dalej.
3. Gdy dalsze atomy połączone są wiązaniami wielokrotnymi, to traktujemy je jakby były wielokrotnie połączone wiązaniami pojedynczymi. Dotyczy to również podstawników aromatycznych, dla których rozpatrujemy jedną ze struktur Kekulégo (nie ma znaczenia którą – wyniki będą równoważne).
4. Jeżeli podstawniki są enancjomerami, to pierwszeństwo ma ten z konfiguracją R.

W praktyce szkolnej do określania konfiguracji absolutnej w przytłaczającej większości wypadków wystarczą pierwsze dwie reguły.

Teraz ujawnia się ogromna przewaga „Atomków” nad rysunkami na kartce papieru. Samodzielnie budując model cząsteczki uczeń od razu dostrzeże, że cząsteczka ma centrum chiralności, bez większego problemu ustali pierwszeństwo podstawników, a następnie, chwytając za podstawnik najmniej ważny, w kilka sekund określi konfigurację absolutną. Szybko też zauważy, że aby otrzymać cząsteczkę o konfiguracji przeciwnej wystarczy zamienić miejscami dowolne dwa podstawniki.

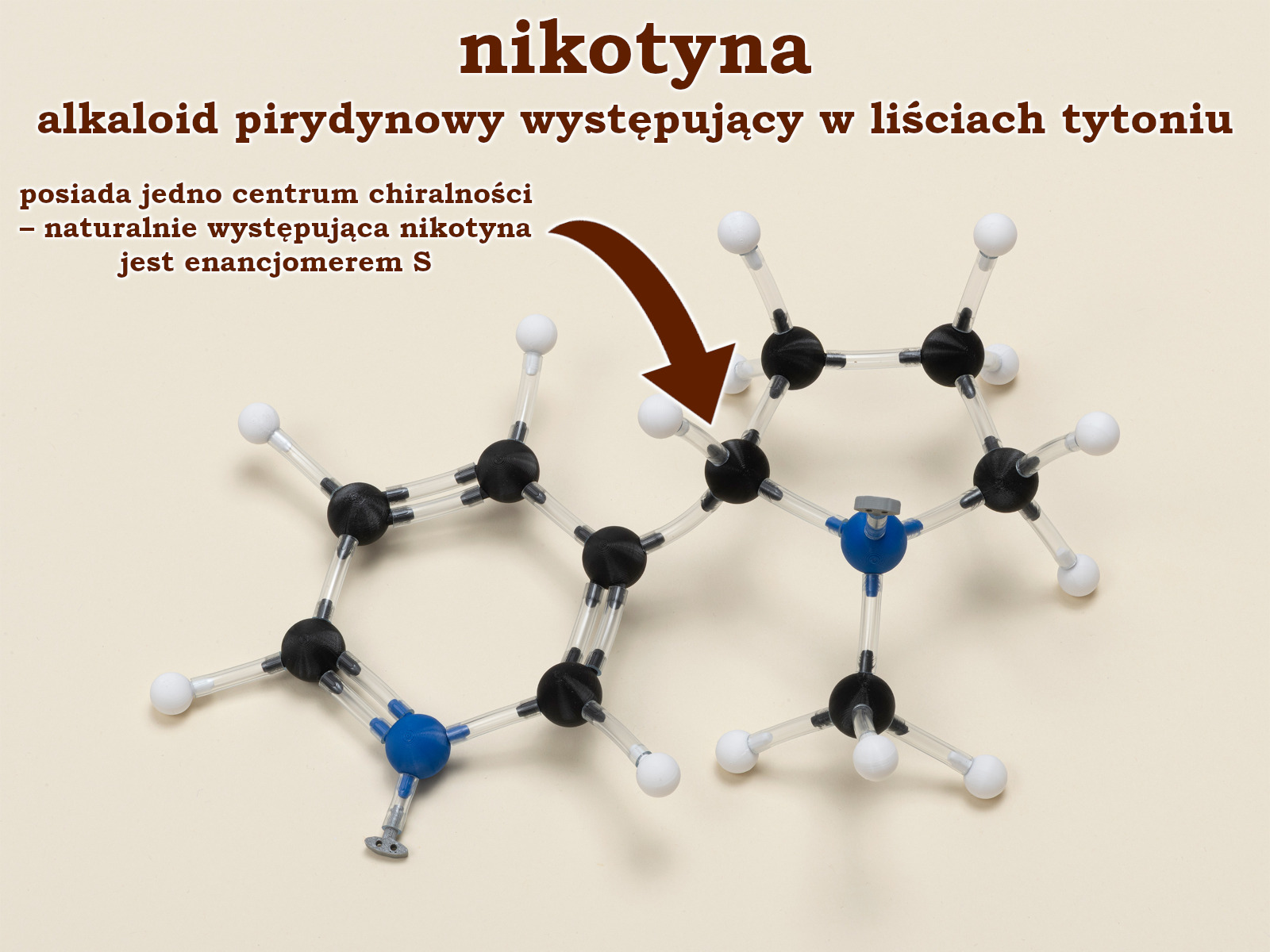
Na przykładzie widocznej wyżej cząsteczki nikotyny pokażemy jak ćwiczyć na większych strukturach.

Układając cząsteczkę uczeń powinien sam zidentyfikować jej centrum chiralności. Następnie należy określić ważność podstawników (tu potrzebne będą trzy pierwsze reguły). Zostaje najłatwiejsze zadanie – chwytamy za najmniej ważny podstawnik (atom wodoru) i patrząc na cząsteczkę od drugiej strony ustalamy konfigurację absolutną. Na koniec możemy jeszcze spróbować przebudować cząsteczkę tak, aby konfiguracja uległa zmianie na przeciwskrętną. Nauka może być prosta i przyjemna!

Konfiguracja absolutna a skręcalność

Konfiguracja absolutna (bezwzględna) to tylko konwencja opisu cząsteczki tak, aby nie trzeba było jej każdorazowo rysować i aby jej budowa była jednoznaczna dla odbiorcy. Nie ma więc ona bezpośredniego związku z rzeczywistą skręcalnością optyczną enancjomeru. W przypadku jednego związku prawoskrętny może okazać się enancjomer o konfiguracji R, a w przypadku innego związku – enancjomer o konfiguracji S.

Skręcalność optyczna jest rzeczywistą własnością fizyczną substancji – taką jak np. jej temperatura topnienia. Wyznaczenie jej odbywa się więc wyłącznie za pomocą eksperymentu.

Zatem aby podać pełną nazwę optycznie czynnego związku należy podać zarówno jego konfigurację (aby jednoznacznie określić budowę jego cząsteczki) oraz kierunek skręcenia (aby jednoznacznie określić jego skręcalność optyczną). Na przykład: (S)‑(—)‑2‑metylo‑1‑butanol.

Wskazówki praktyczne

Do rozważań na temat izomerii optycznej „Atomki” są wręcz wymarzoną pomocą. Nadaje się do tego każdy z dostępnych zestawów organicznych. Paradoksalnie – zestawy uproszczone przeznaczone dla szkoły podstawowej mogą nawet sprawdzać się lepiej ze względu na szybszą budowę podstawników zawierających heteroatomy i halogeny (brak konieczności uzupełniania par elektronowych).

Kupując zestaw dla licealisty warto, oczywiście, kupić organiczny zestaw Lewisa ze względu na możliwość budowy struktur zgodnych z teorią oktetu elektronowego. Jednak nic nie stoi na przeszkodzie aby rozszerzyć go dodatkowo 200‑elementowym zestawem dla szkół podstawowych. Wszystkie zestawy można łączyc ze sobą. Zabieg ten pozwoli budować duże cząsteczki eksponując pary elektronowe wyłącznie w tych miejscach, gdzie ma to wpływ na właściwości budowanego związku chemicznego.

Łukasz Aranowski
4 grudnia 2024